Introductie extreme waarde statistiek met python

Disclaimer: ik ben geen statisticus.

Ik was op zoek naar extreme waarde statistiek voor onze debietreeksen (bij het waterschap). In een vorig leven (lees universiteit) heb ik wel is extreme waarde statistiek toegepast met de R-package extRemes (aanrader), omdat ik op mijn werk enkel beschikking heb tot python, het nu in python geprobeerd. Het bleek lastig om goede voorbeelden en packages te vinden, vandaar dit artikel.

Extreme waarde statistiek, wat is dat?

Op naar Wikipedia
In de kansrekening en de statistiek is een extreme waarde het maximum of het minimum in een aselecte steekproef. In de theorie over extreme waarden bestudeert men de mogelijke verdeling van de extreme waarden.

Centraal in de theorie staat het resultaat dat onder bepaalde voorwaarden als limietverdeling voor een extreme waarde slechts drie verdelingen mogelijk zijn, onafhankelijk van de oorspronkelijke verdeling in de steekproef.

Ok, ok, extreme waarde statistiek gaat dus over evenementen die ver afwijken van het standaard gedrag, klinkt logisch, extremen. Daarbij is er ook vaak het doel om iets te zeggen over extremen die we nog niet hebben waargenomen, ofwel extrapolatie. Daarom fitten we een extreme waardeverdeling (zoals bijv. Gumbel) op onze reeds geobserveerde extremen waarden. Als we een extreme waardeverdeling hebben die goed past kunnen we iets zeggen over herhalingstijden en overschrijdingskansen, ook met een herhalingstijd groter dan onze set, super mooi!

Extreme waardestatistiek wordt in de hydrologie bijvoorbeeld toegepast bij extreme neerslag en afvoer. Buiten de hydrologie kan je denken aan bijv. in de klimatologie aan extreme golfhoogtes, tornado’s, maar ook in de bouw of financiele sector wordt extreme waarde statistiek toegepast.

Ik ben vooral geintereseerd in de debieten, de afvoeren van de Rijn bij Lobith lijken mij een mooi startpunt, omdat dit een set is waar iedereen makkelijk bij kan. De set kan je downloaden op Waterinfo.

Data inladen en visualiseren

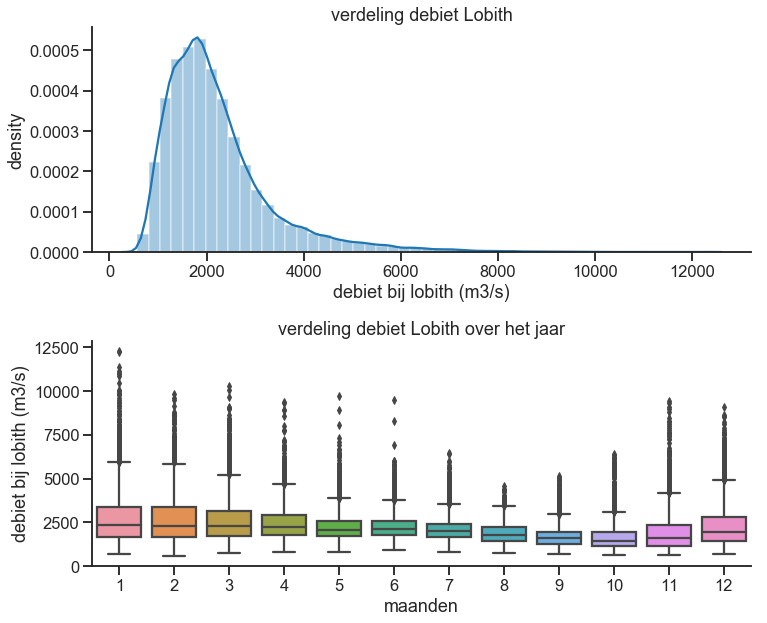
Nu wat python, zie hieronder figuur met verdeling van de debieten (histogram) en verdeling van de debieten over het jaar gemiddeld (boxplot). Lobith heeft een redelijk normale verdeling voor een rivier; de afvoer wordt niet nul en heeft een lange staart naar de extreme kant, meest voorkomende afvoer ligt rond de 2.000 m3/s met extremen naar de 12.000 m3/s. In de verdeling over het jaar zie je dat hogere afvoeren vooral voorkomen van november tot januari (vooral veroorzaakt door regen) en van maart tot juni (veroorzaakt door combinatie van smeltwater en regen). In de maanden juli tot oktober is de afvoer over het algemeen niet extreem.

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import requests

%matplotlib inline

q = pd.read_csv('lobith.csv', sep=';', decimal=',', encoding='iso-8859-1', 
                  parse_dates=[['WAARNEMINGDATUM', 'WAARNEMINGTIJD']],
                  infer_datetime_format=True, dayfirst=True, 
                  usecols=['MEETPUNT_IDENTIFICATIE', 'WAARNEMINGDATUM', 'WAARNEMINGTIJD', 'NUMERIEKEWAARDE'],
                 )
q = q.set_index(['MEETPUNT_IDENTIFICATIE', 'WAARNEMINGDATUM_WAARNEMINGTIJD']) # ik gebruik hier mijn standaard om rws data in 
# te laden dan kan je ook sets met meerdere meetpunten uit een csv in een keer simpel inladen
lobith = q.loc['Lobith'] # juiste meetpunt selecteren
lobith = lobith.resample('d').mean() # 10-min data hebben we niet nodig
lobith = lobith[lobith < 99999] # nan-values zijn niet eenduidig (zitten in de orde 10e36-37) dus selecteer de logische waardes
lobith = lobith.squeeze() # maak er een series van

import seaborn as sns

sns.set_context("talk")
sns.set_style("ticks")

# plotje om idee te krijgen van de reeks
fig, ax = plt.subplots(2, 1, figsize=(11,9))
sns.distplot(lobith.dropna().values, ax=ax[0], norm_hist=True)
ax[0].set_title('verdeling debiet Lobith')
ax[0].set_ylabel('density')
ax[0].set_xlabel('debiet bij lobith (m3/s)')
sns.boxplot(x=lobith.index.month.values, y=lobith.values, ax=ax[1])
ax[1].set_title('verdeling debiet Lobith over het jaar')
ax[1].set_xlabel('maanden')
ax[1].set_ylabel('debiet bij lobith (m3/s)')
sns.despine()
fig.tight_layout();

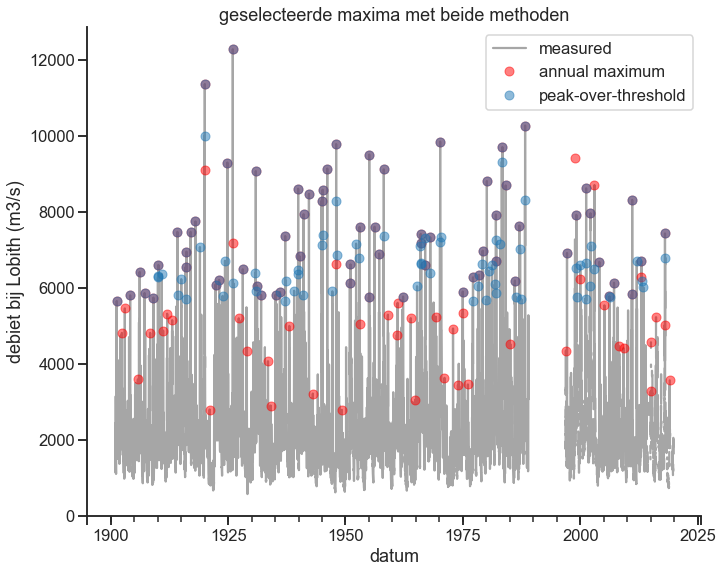
Jaarlijkse maxima of peak-over-threshold

De makkelijkste manier om extremen te selecteren is om de maximale afvoer van elk jaar te selecteren, dit kan simpel in pandas door bijvoorbeeld te resamplen. Peak-over-threshold is iets lastigere methode omdat je alleen onafhankelijke evenementen wil selecteren, een extreme afvoer kan (en zal meestal) meerdere dagen duren, je wil dan enkel het maximum hebben. Gelukkig heeft scipy een oplossing find_peaks, hier kan je een distance aangeven ofwel hoever dienen pieken minimaal uit elkaar te liggen. Je peak-over-threshold zou een vergelijkbaar aantal extreme waarden moeten hebben als het aantal jaar, dus speel een beetje met de quantiles.

from scipy.signal import find_peaks

am = lobith.loc[lobith.groupby(lobith.index.year).idxmax().dropna().values] # annual maximum methode, groepeer per jaar en 
# gebruik de index van het maxima
pot = lobith.iloc[find_peaks(lobith, height=lobith.quantile(0.98), distance=7)[0]] #peak-over-threshold methode, gebruikt
# kwantielen om een indicatie te krijgen voor hoge afvoeren, hier 98% kwantiel, en pieken moeten minimaal een week uit elkaar
# liggen

print('lengte annual maximum:', len(am), ' lengte peak-over-threshold:', len(pot))

lengte annual maximum: 112  lengte peak-over-threshold: 131

ax = lobith.plot(figsize=(16,11), label='measured', color='grey', alpha=0.7)
am.plot(style='o', ax=ax, label='annual maximum', c='red', alpha=0.5)
pot.plot(style='o', ax=ax, label='peak-over-threshold', alpha=0.5)
ax.set_ylabel('debiet bij Lobith (m3/s)')
ax.set_xlabel('datum')
ax.set_title('geselecteerde maxima met beide methoden')
sns.despine()
plt.legend();

De statistiek

Nu zijn we eindelijk aangekomen de statistiek, ik heb de package lmoments3 gebruikt, deze kan wat ik wil, een fit maken op basis van een set extremen. Hieronder de resultaten voor 3 van de bekendere extremewaarde verdelingen voor debieten, voor zowel de annual maxima methode als de peak-over-threshold methode. De package heeft nog veel meer verdelingen om mee te spelen.

from lmoments3 import distr

fig, ax = plt.subplots(1, 2, figsize=(15,9))
for idx, data in enumerate([pot, am]):
    theta = distr.gev.lmom_fit(data) # fit gev op de geprepareerde pot-data
    gev = distr.gev(**theta) # bereken de verdeling met de parameters uit de fit
    theta = distr.gum.lmom_fit(data)
    gum = distr.gum(**theta)
    theta = distr.pe3.lmom_fit(data)
    pe3 = distr.pe3(**theta)

    T = np.arange(1, 999.1, 0.1) + 1 # herhalingstijden van T1 tot T1000
    ax[idx].plot(T, gev.ppf(1.0-1./T), 'g', label='GEV') # ppf ofwel percent point feature, gebruiken om de debieten bij de herhalings
    # tijden te bepalen, 1.0-1./T -> overschrijdingskans
    ax[idx].plot(T, gum.ppf(1.0-1./T), 'r', label='Gumbel')
    ax[idx].plot(T, pe3.ppf(1.0-1./T), 'b', label='Pearson 3')

    N = np.arange(1, len(data)+1, 1.0) # array met van 1 tot n+1, 1.0 want moeten floats zijn
    Nmax = max(N) # aantal datapunten + 1

    ax[idx].scatter(Nmax/N, sorted(data)[::-1], color = 'black', facecolors='none', label='Empirical') # T = rank datapunt / 
    # (1 + lengte datapunten), daarom dus punten sorteren van hoog naar laag en bijbehorende herhalings tijd is idx / Nmax
    ax[idx].set_xscale('log')
    ax[idx].set_xlabel('Herhalingstijd logaritmisch (jaar)')
    ax[idx].legend()
ax[0].set_ylabel('Debiet bij Lobith (m3/s)')
ax[0].set_title('Peak-over-Threshold')
ax[1].set_title('Annual Maximum')
fig.suptitle('Extreme waarde statistiek afvoer bij Lobith (T1-T100)')
sns.despine()
plt.show()

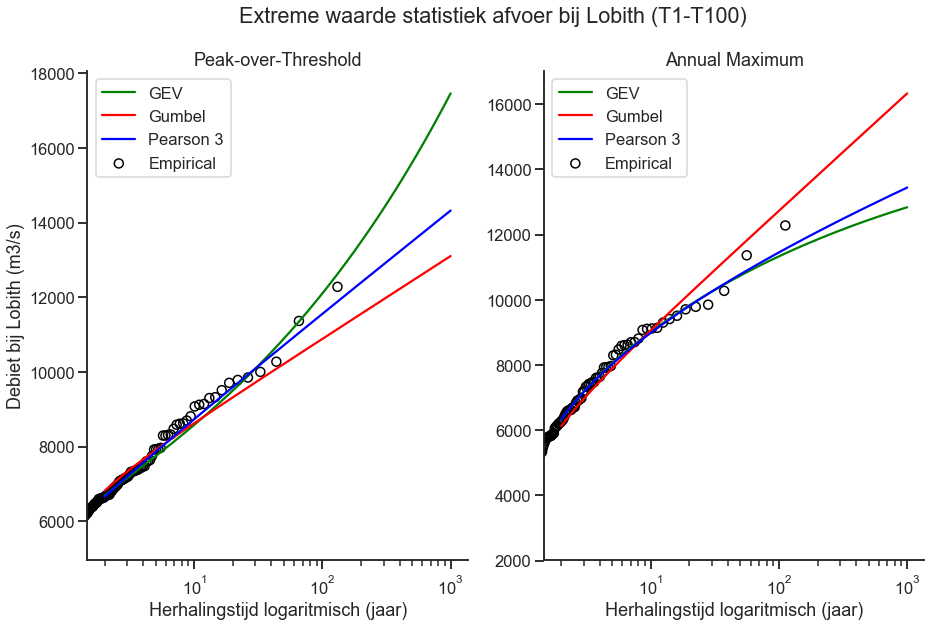
Conclusie

Zoals je in het plaatje hierboven kan zien zijn er flinke verschillen tussen de geselecteerde verdelingen en tussen de annual maxima en pot methode. Voor een herhalingstijd T1000, zijn waardes tussen de 12.000 en 18.000 m3/s bepaald, dit is een groot bereik. Je zou de analyse nog verder uit kunnen breiden door bijvoorbeeld samples uit de reeks (bootstrapping) te gebruiken, hiermee zou je ook een bandbreedte (confidence interval) kunnen bepalen.